№
п/п | Наименование параметра | Формула | Обозначения |
|---|
| 1.1 | Средняя скорость | 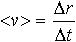 | Δr ― перемещение материальной точки за интервал времени Δt. |
| 1.2 | Средняя путевая скорость | 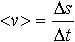 | Δs ― путь, пройденный материальной точки за интервал времени Δt. |
| 1.3 | Мгновенная скорость | 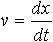 | x ― координата, t ― время |
| 1.4 | Ускорение | 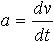 | v ― скорость, t ― время |
| 1.5 | Полное ускорение | 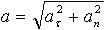 | aτ ― тангенциальное ускорение, an ― нормальное ускорение |
| 1.6 | Тангенциальное ускорение | 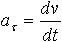 | v ― скорость, t ― время |
| 1.7 | Нормальное ускорение | 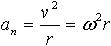 | v ― скорость тела, r ― радиус кривизны траектории, ω ― угловая скорость |
| 1.8 | Уравнение равномерного движения вдоль оси х | 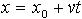 | х0 ― начальная координата, v ― скорость тела, x ― координата в момент времени t |
| 1.9 | Кинематическое уравнение равнопеременного движения вдоль оси х | 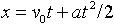 | v0 ― начальная скорость тела, a ― ускорение тела, v ― скорость тела в момент времени t |
| 1.10 | Средняя угловая скорость | 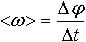 | Δφ ― изменение угла поворота за интервал время Δt |
| 1.11 | Мгновенная угловая скорость | 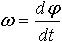 | φ ― угол поворота, t ― время |
| 1.12 | Угловое ускорение | 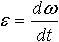 | ω ― угловая скорость, t ― время |
| 1.13 | Кинематическое уравнение равномерного вращения | 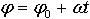 | φ0 ― начальный угол поворота, ω ― угловая скорость, t ― время |
| 1.14 | Частота вращения | 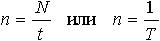 | N ― число оборотов, совершаемых телом за время t, T ― период вращения |
| 1.15 | Кинематическое уравнение равнопеременного вращения | 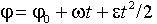 | φ0 ― начальный угол поворота, ω ― угловая скорость, ε ― угловое ускорение, t ― время |
| 1.16 | Угловая скорость тела при равномерном вращении | 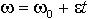 | ω0 ― угловая скорость, ε ― угловое ускорение, t ― время |
| 1.17 | Линейная скорость точки | 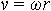 | ω ― угловая скорость, r ― радиус кривизны траектории |
| 1.18 | Длина пути, пройденного точкой по дуге окружности радиусом r | 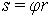 | φ ― угол поворота тела, r ― радиус кривизны траектории |
| 1.19 | Нормальное ускорение точки | 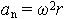 | ω ― угловая скорость, r ― радиус кривизны траектории |
| 1.20 | Тангенциальное ускорение точки | 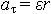 | ε ― угловое ускорение, r ― радиус кривизны траектории |
| 1.21 | Второй закон Ньютона | 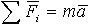 | 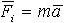 ― геометрическая сумма сил, действующих на материальную точку, m ― масса, a ― ускорение ― геометрическая сумма сил, действующих на материальную точку, m ― масса, a ― ускорение |
| 1.21a | Пример применения второго закона Ньютона
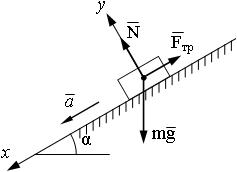 | 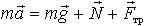
или в проекции на оси координат:
на x
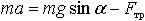
на y
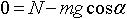 | 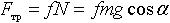 ― сила трения, f ― коэффициент трения, g = 9,81 м/с2 ― ускорение свободного падения ― сила трения, f ― коэффициент трения, g = 9,81 м/с2 ― ускорение свободного падения |
| 1.22 | Сила упругости | 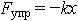 | k ― коэффициент упругости (жесткость в случае пружины), x ― абсолютная деформация |
| 1.23 | Гравитационная сила | 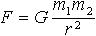 | G = 6,67∙10−11 м3/(кг∙с2) ― гравитационная постоянная, m1 и m2 ― массы взаимодействующих тел, r ― расстояние между ними |
| 1.24 | Координаты центра масс системы материальных точек | 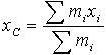 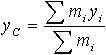 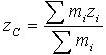 | mi ― масса i-й материальной точки; xi, yi, zi ― ее координаты |
| 1.25 | Закон сохранения импульса | 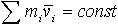 | mi ― масса i-й материальной точки, vi ― ее скорость |
| 1.25a | Пример. Закон сохранения импульса для ядра, которое распалось на два осколка.
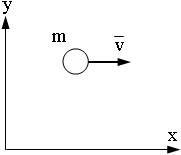
Рис. 1 - ядро до разрыва
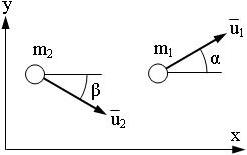
Рис. 2 - осколки после разрыва ядра | 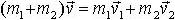
или в проекции на оси координат:
на x
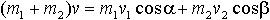
на y
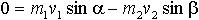 | m1 ― масса первого осколка, m2 ― масса второго осколка, v ― скорость ядра, v1 и v2 ― скорости осколков после распада ядра, α и β ― углы отклонения направления движения частиц от первоначального направления движения ядра |
| 1.26 | Работа, совершаемая постоянной силой | 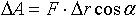 | α ― угол между направлениями векторов силы 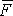 и перемещения и перемещения 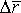 |
| 1.27 | Работа, совершаемая постоянной силой | 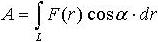 | интегрирование ведется вдоль траектории, обозначаемой L |
| 1.28 | Средняя мощность за интервал времени Δt | 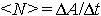 | ΔA ― работа за время Δt |
| 1.29 | Мгновенная мощность | 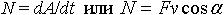 | dA ― работа за время dt |
| 1.30 | Кинетическая энергия материальной точки | 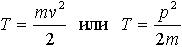 | m ― масса материальной точки, v ― скорость материальной точки, р ― импульс |
| 1.31 | Потенциальная энергия П тела и сила F, действующая на тело в данной точке поля, связаны соотношением | 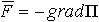
или
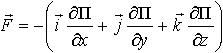 | 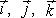 ― единичные векторы, x, y, z ― координаты точки поля ― единичные векторы, x, y, z ― координаты точки поля |
| 1.32 | Если поле сил обладает сферической симметрией | 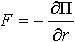 | r ― координата в сферической системе координат |
| 1.33 | Потенциальная энергия упруго деформированного тела | 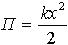 | k ― коэффициент упругости (жесткость в случае пружины), x ― абсолютная деформация |
| 1.34 | Потенциальная энергия гравитационного взаимодействия двух материальных точек массами m1 и m2, находящихся на расстоянии r друг от друга | 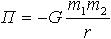 | G = 6,67∙10−11 м3/(кг∙с2) ― гравитационная постоянная, m1 и m2 ― массы взаимодействующих тел, r ― расстояние между ними |
| 1.35 | Основное уравнение динамики вращательного движения твердого тела относительно неподвижной оси | 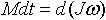 | М ― момент силы, действующей на тело, ω ― угловая скорость, Jω ― момент импульса, dt ― приращение времени |
| 1.36 | Уравнение вращательного движения (при J = const) | 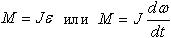 | М ― момент силы, действующей на тело, J ― момент инерции, ε ― угловое ускорение, ω ― угловая скорость, t ― время |
| 1.37 | Момент инерции однородного тонкого стержня, ось вращения которого проходит через центр масс стержня перпендикулярно стержню | 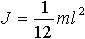 | m ― масса стержня, l ― длина стержня |
| 1.38 | Момент инерции однородного тонкого стержня, ось вращения которого проходит через конец стержня перпендикулярно стержню | 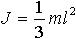 | m ― масса стержня, l ― длина стержня |
| 1.39 | Момент инерции однородного диска, ось вращения которого проходит через центр диска перпендикулярно диску | 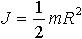 | m ― масса диска, R ― радиус диска |
| 1.40 | Момент инерции однородного шара, ось вращения которого проходит через центр шара | 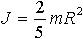 | m ― масса шара, R ― радиус шара |
| 1.41 | Теорема Штейнера: момент инерции тела относительно произвольной оси равен |  | J0 ― момент инерции этого тела относительно оси, проходящей через центр тяжести тела параллельно заданной оси, а ― расстояние между осями, m ― масса тела |
| 1.42 | Закон сохранения момента импульса | 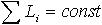 | Li = Jiωi ― момент импульса тела с номером i, входящего в состав системы |
| 1.43 | Работа постоянного момента силы М, действующего на вращающееся тело | 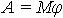 | φ ― угол поворота тела |
| 1.44 | Мгновенная мощность, развиваемая при вращении тела | 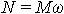 | М ― вращающий момент, ω ― угловая скорость тела |
| 1.45 | Кинетическая энергия вращающегося тела | 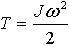 | J ― момент инерции тела, ω ― угловая скорость тела |
| 1.46 | Кинетическая энергия тела, катящегося без скольжения | 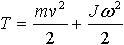 | m ― масса тела, v ― скорость центра инерции тела, J ― момент инерции тела, ω ― угловая скорость тела |
| 1.47 | Уравнение гармонических колебаний
Скорость точки изменяется по закону
Ускорение точки изменяется по закону | 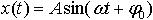
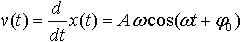
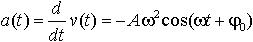 | A ― амплитуда колебаний, ω ― круговая частота, t ― время, φ ― начальная фаза |
| 1.48 | Амплитуда A результирующего колебания, полученного при сложении двух колебаний с одинаковыми частотами, происходящих по одной прямой
Начальная фаза φ результирующего колебания | 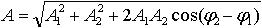
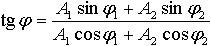 | A1 и A2 ― амплитуда составляющих колебаний, φ1 и φ2 ― их начальные фазы |
| 1.49 | Уравнение затухающих колебаний | 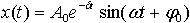 | А0 ― амплитуда колебаний в момент t = 0; δ ― коэффициент затухания; ω ― циклическая частота колебаний; φ0 ― начальная фаза |
| 1.50 | Зависимость амплитуды затухающих колебаний от времени | 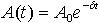 | А0 ― амплитуда колебаний в момент t = 0; δ ― коэффициент затухания |
| 1.51 | Логарифмический декремент колебаний | 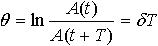 | где A(t) и A(t+T) ― амплитуды двух последовательных колебаний, отстоящих по времени друг от друга на период Т |
| 1.52 | Акустический эффект Доплера | 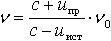 | ν ― частота звука, воспринимаемого движущимся прибором (или ухом); с ― скорость звука в среде; uпр ― скорость прибора относительно среды; uист ― скорость источника звука относительно среды; ν0 ― частота звука, испускаемого источником |
| 1.53 | Уравнение колебаний волны | 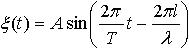 | ξ ― смещение колеблющейся точки на расстоянии l от источника колебаний в момент времени t; T ― период колебаний; λ ― длина волны |
| 1.54 | Период колебаний тела, подвешенного на пружине (пружинный маятник) | 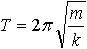 | m ― масса тела, k ― жесткость пружины |
| 1.55 | Период колебаний математического маятника | 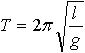 | l ― длина маятника, g ― ускорение свободного падения |
| 1.56 | Период колебаний физического маятника | 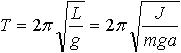 | J ― момент инерции колеблющегося тела относительно оси колебаний, a ― расстояние центра масс маятника от оси колебаний; L = J/(ma) ― приведенная длина физического маятника |
| 1.57 | Период крутильных колебаний тела, подвешенного на упругой нити | 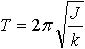 | J ― момент инерции тела относительно оси, совпадающей с упругой нитью; k ― жесткость упругой нити, равная отношению упругого момента, возникающего при закручивании нити, к углу, на который нить закручивается |