Формулы для решения задач по физике
ЭЛЕКТРИЧЕСТВО
№
п/п | Наименование параметра | Формула | Обозначения |
|---|
| 3.1 | Закон Кулона | 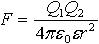 | Q1 и Q2 ― точечные заряды, ε0 = 8,85∙10−12 Ф/м ― электрическая постоянная, ε ― диэлектрическая проницаемость среды, r ― расстояние между зарядами |
| 3.2 | Емкость плоского конденсатора | 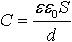 | ε ― диэлектрическая проницаемость среды между пластинами, ε0 = 8,85∙10−12 Ф/м ― электрическая постоянная, S ― площадь пластины, d ― расстояние между пластинами |
| 3.3 | Емкость сферического конденсатора | 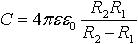 | ε ― диэлектрическая проницаемость среды между сферами, ε0 = 8,85∙10−12 Ф/м ― электрическая постоянная, R1 и R2 ― радиусы внутренней и внешней сфер соответственно |
| 3.4 | Потенциал электрического поля, созданного точечным зарядом | 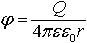 | Q ― точечный заряд, ε ― диэлектрическая проницаемость среды, ε0 = 8,85∙10−12 Ф/м ― электрическая постоянная, r ― расстояние от точечного заряда |
| 3.5 | Потенциал электрического поля, созданного металлической сферой на расстоянии r от центра сферы:
внутри сферы и на поверхности
(r ≤ R)
вне сферы (r > R) |
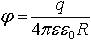
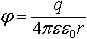 | q ― заряд сферы, R ― радиус сферы, ε ― диэлектрическая проницаемость среды, ε0 = 8,85∙10−12 Ф/м ― электрическая постоянная, r ― расстояние от центра сферы |
| 3.6 | Теорема Гаусса-Остроградского | 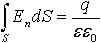 | S ― площадь гауссовой поверхности, Еn ― нормальная к поверхности составляющая вектора напряженности электростатического поля, Q ― заряд, охваченный поверхностью интегрирования, ε ― диэлектрическая проницаемость среды, ε0 = 8,85∙10−12 Ф/м ― электрическая постоянная |
| 3.7 | Напряженность поля, создаваемого зарядом бесконечной пластины | 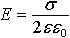
вывод формулы | σ ― поверхностная плотность заряда, ε ― диэлектрическая проницаемость среды, ε0 = 8,85∙10−12 Ф/м ― электрическая постоянная, r ― расстояние от пластины |
| 3.8 | Напряженность электрического поля, создаваемого металлической заряженной сферой:
внутри сферы (r < R)
на поверхности сферы (r = R)
вне сферы (r > R) |
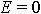
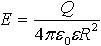
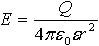 | Q ― заряд сферы; ε ― диэлектрическая проницаемость среды; ε0 = 8,85∙10−12 Ф/м ― электрическая постоянная; R ― радиус сферы; r ― расстояние от центра сферы |
| 3.9 | Напряженность электрического поля, создаваемого бесконечно длинной равномерно заряженной нитью (или цилиндром) | 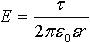
вывод формулы | τ ― линейная плотность заряда; ε ― диэлектрическая проницаемость среды между пластинами, ε0 = 8,85∙10−12 Ф/м ― электрическая постоянная, r ― расстояние от оси нити |
| 3.10 | Энергия конденсатора | 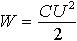 | С ― емкость конденсатора; U ― напряжение на пластинах |
| 3.11 | Сопротивление провода | 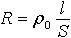 | ρ0 ― удельное сопротивление материала провода, S ― площадь сечения провода;
для меди ρ0 = 0,0175∙10−6 Ом∙м;
для алюминия ρ0 = 0,028∙10−6 Ом∙м;
для вольфрама ρ0 = 0,055∙10−6 Ом∙м;
для железа ρ0 = 0,1∙10−6 Ом∙м |
| 3.12 | Работа, совершаемая электрическим полем при перемещении точечного заряда q из точки 1 поля в точку 2 | 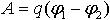 | φ1 и φ2 ― потенциалы точек 1 и 2 соответственно |
| 3.13 | Электрический момент диполя | 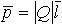 | |
| 3.14 | Напряженность поля точечного диполя
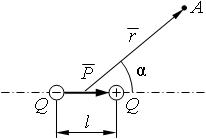 | 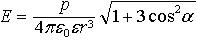 | р ― электрический момент диполя; r ― абсолютное значение радиус-вектора, проведенного от центра диполя к точке, напряженность поля в которой нас интересует; α ― угол между радиус-вектором 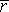 и плечом и плечом 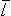 диполя; ε ― диэлектрическая проницаемость; ε0 ― электрическая постоянная диполя; ε ― диэлектрическая проницаемость; ε0 ― электрическая постоянная |
| 3.15 | Напряженность поля точечного диполя в точке, лежащей на оси диполя (α = 0)
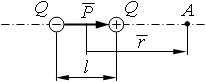 | 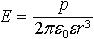 | р ― электрический момент диполя; r ― абсолютное значение радиус-вектора, проведенного от центра диполя к точке, напряженность поля в которой нас интересует; ε ― диэлектрическая проницаемость; ε0 ― электрическая постоянная |
| 3.16 | Напряженность поля точечного диполя в точке, лежащей на перпендикуляре к плечу диполя, восстановленном из его середины
(α = π/2)
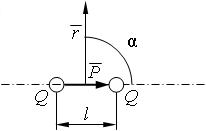 | 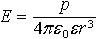 | р ― электрический момент диполя; r ― абсолютное значение радиус-вектора, проведенного от центра диполя к точке, напряженность поля в которой нас интересует; ε ― диэлектрическая проницаемость; ε0 ― электрическая постоянная |
| 3.17 | Потенциал поля точечного диполя
 | 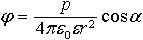 | р ― электрический момент диполя; r ― абсолютное значение радиус-вектора, проведенного от центра диполя к точке, напряженность поля в которой нас интересует; α ― угол между радиус-вектором 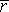 и плечом и плечом 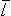 диполя; ε ― диэлектрическая проницаемость; ε0 ― электрическая постоянная диполя; ε ― диэлектрическая проницаемость; ε0 ― электрическая постоянная |
| 3.18 | Потенциал поля точечного диполя в точке A, лежащей на оси диполя
 | 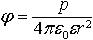 | р ― электрический момент диполя; r ― абсолютное значение радиус-вектора, проведенного от центра диполя к точке, напряженность поля в которой нас интересует; ε ― диэлектрическая проницаемость; ε0 ― электрическая постоянная |
| 3.19 | Механический момент, действующий на диполь | 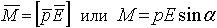 | 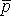 ― электрический момент диполя, ― электрический момент диполя, 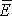 ― напряженность однородного электрического поля, α ― угол между направлениями векторов ― напряженность однородного электрического поля, α ― угол между направлениями векторов 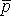 и и 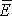 |
| 3.20 | Период колебаний колебательного контура | 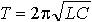 | L ― индуктивность катушки, C ― емкость конденсатора |
|