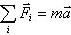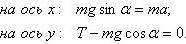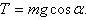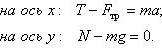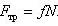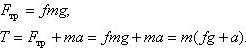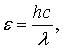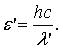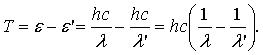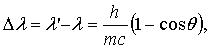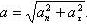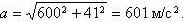В разделе Физика можно найти решения контрольных задач по физике и тестов с подробными объяснениями. В решении, где необходимо, приводится рисунок.
Если требуется вывод формулы, которая использована в задаче, смотрите в разделе Формулы.
Если под текстом задачи кроме кнопки "Решение" есть кнопка "Изменить числа в условии", значит по кнопке можно перейти на страницу с выбором чисел для данной задачи. То есть решить задачу по "дано" онлайн. Затем после нажатия кнопки "Решить" программа сайта решит задачу и сформирует файл word с решением, а вам предложит выбрать способ оплаты. После оплаты на сайте платежной системы следует нажать ссылку "Вернуться в магазин" или "Перейти к продавцу" и вы перейдете на страницу, где вас ждет ссылка на скачивание только что решенной задачи.
Средняя цена задачи по физике около 34 руб..
Файл с решением задачи набран в Word 2003 и заархивирован в zip-архив. Шрифт 14px (Times New Roman).
Другие предметы здесь
Часто задаваемые вопросы по решению задач|
Как найти силу натяжения нити?
Что такое задерживающая разность потенциалов?
Что такое кинетическая энергия электрона отдачи?
Как определить нормальное, тангенциальное и полное ускорение движущейся точки?
|
Как найти силу натяжения нити?
Для силы натяжения нити нет готовой формулы. Для каждой задачи получается своя формула этой силы. Нужно нарисовать тело (или тела), к которому прикреплена нить, указать на рисунке силы, действующие на тело (тела). В уравнение, составленное на основании II закона Ньютона, войдет и сила натяжения нити. Отсюда ее и нужно выразить. Рассмотрим два примера.
|
Задача 1.
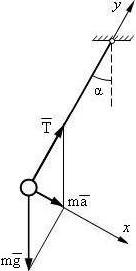
Тело массой m колеблется на нити длиной l. Максимальный угол отклонения нити равен α. Найти силу натяжения нити в наивысшей точке траектории тела.
Решение.
Выбираем оси координат, чтобы одна из них (Oy) была параллельна нити. Записываем второй закон Ньютона
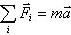
в проекции на оси координат:
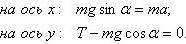
Из второго уравнения находим силу натяжения нити:
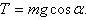
|
| |
Задача 2.
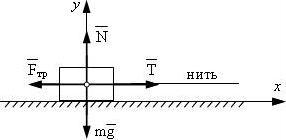
Тело массой m тянут за горизонтально натянутую нить по горизонтальной плоскости с ускорением a. Коэффициент трения f. Найти силу натяжения нити.
Решение.
На основании второго закона Ньютона записываем:
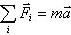
или в проекции на оси координат:
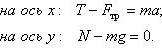
Дополнительное уравнение:
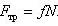
Здесь T — сила натяжения нити, Fтр — сила трения, N — сила упругости стола, mg — сила тяжести.
Исключаем N и Fтр и находим силу натяжения нити:
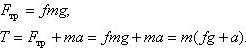
Обратите внимание на то, что формулы для T в первой и второй задаче разные. Значит нет общей формулы для силы натяжения нити.
|
|
Что такое задерживающая разность потенциалов?
Задерживающая разность потенциалов — напряжение между катодом и анодом, приложенное таким образом, чтобы противодействовать движению электронов от катода к аноду.
|
Этот термин часто используется в опытах с фотоэффектом. В стеклянный баллон, из которого выкачан воздух, впаивают два электрода ― К и А (рис. 1). Внутрь баллона через кварцевое "окошко", прозрачное для ультрафиолетового излучения, направляют свет на катод К. Подаваемое на электроды напряжение можно изменять с помощью потенциометра и измерять вольтметром V. Под действием света катод испускает электроны, которые замыкают цепь между электродами, и амперметр фиксирует наличие тока в цепи. Измеряя ток и напряжение, можно построить график зависимости силы фототока от напряжения между электродами I = I(U) (рис. 2).
| 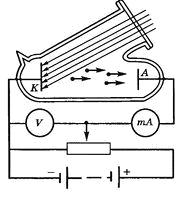
Рис.1
|
Из графика следует, что:
а) при отсутствии напряжения между электродами фототок отличен от нуля, что можно объяснить наличием у фотоэлектронов при вылете кинетической энергии.
б) При некотором значении напряжения между электродами UH сила фототока перестает зависеть от напряжения, т.е. достигает насыщения IH.
в) Если катод соединить с положительным полюсом источника тока, а анод — с отрицательным, то в электростатическом поле между электродами фотоэлектроны будут тормозиться, а сила фототока уменьшаться при увеличении значения этого отрицательного напряжения. При некотором значении отрицательного напряжения UЗ (его называют задерживающим напряжением) фототок прекращается.
Задачи на задерживающую разность потенциалов.
|
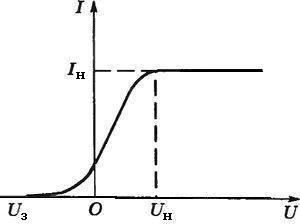
Рис.2
|
Что такое кинетическая энергия электрона отдачи?
Пучок фотонов направляют на электронный газ. Фотон, сталкиваясь с электроном, передает ему часть своей энергии. При этом считается, что электрон до столкновения с фотоном не обладал кинетической энергией. Кинетическая энергия, которую приобрел электрон, и есть кинетическая энергия электрона отдачи. Она равна энергии, которую утратил фотон.
Фотон до рассеяния обладал энергией
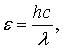
после рассеяния энергией
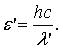
Значит кинетическая энергия электрона отдачи равна
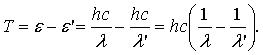
Иногда (если известен угол θ рассеяния фотона или его нужно найти) к этому уравнению добавляется формула Комптона, описывающая изменение длины волны фотона при рассеянии его на свободном электроне на угол θ:
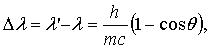
где m = 9,11·10–31 кг — масса электрона отдачи; λ и λ' — длины волн падающего и рассеянного фотона; c = 3·108 м/с — скорость света в вакууме; h = 6,63·10–34 Дж·с — постоянная Планка.
Получили систему уравнений, из которой можно найти кинетическую энергию электрона отдачи.
Задачи на энергию электрона отдачи.
|
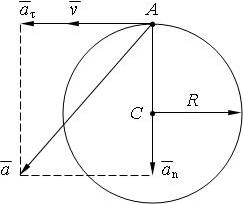
Как определить нормальное, тангенциальное и полное ускорение движущейся точки?
По формулам:
an = v2/R, где v — скорость точки, R — радиус кривизны траектории;
aτ = dv/dt, где v — скорость как функция времени t;
a2 = aτ2 + an2.
| |
Пример 3.
Точка движется по окружности радиуса R = 24 м со скоростью, которая изменяется по закону v(t) = 3t2+5t–18. Найти нормальное, тангенциальное и полное ускорение точки в момент времени t = 6 с.
Решение.
Вычислим скорость точки в момент времени t = 6 с:
v(6) = 3·62+5·6–18 = 120 м/с.
Нормальное ускорение точки в момент времени t = 6 c равно
an(6) = v2/R = 1202/24 = 600 м/c2.
Найдем производную функции скорости по времени:
aτ = dv/dt = 6t+5.
Тангенциальное ускорение в момент времени t = 6 c равно
aτ(6) = 6·6+5 = 41 м/с2.
Полное ускорение равно
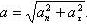
Полное ускорение точки в момент времени t = 6 c равно
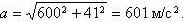
|
|
Владелец сайта: WMID 302130364734 моб. +380635848153 Олег e-mail: sdelaemna5@gmail.com
Правовая информация
|