найти доверительный интервал оценки математического ожидания

---

Задача 197tv

Найти доверительный интервал для оценки математического ожидания m нормального распределения с надёжностью 0,95, зная выборочную среднюю х, объём выборки n и среднее квадратическое отклонение.
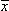= 75,08; σ = 15; n = 225; γ = 0,95.

Решение

---

Задача 199tv

Найти доверительный интервал для оценки математического ожидания m нормального распределения с надёжностью 0,95, зная выборочную среднюю х, объём выборки n и среднее квадратическое отклонение.
= 75,10; σ = 13; n = 169; γ = 0,95.

Решение

---

Задача 200tv

Найти доверительный интервал для оценки математического ожидания m нормального распределения с надёжностью 0,95, зная выборочную среднюю х, объём выборки n и среднее квадратическое отклонение.
= 75,11; σ = 12; n = 144; γ = 0,95.

Решение

---

Задача 201tv

Найти доверительный интервал для оценки математического ожидания m нормального распределения с надёжностью 0,95, зная выборочную среднюю х, объём выборки n и среднее квадратическое отклонение.
= 75,12; σ = 11; n = 121; γ = 0,95.

Решение

---

Задача 202tv

Найти доверительный интервал для оценки математического ожидания m нормального распределения с надёжностью 0,95, зная выборочную среднюю х, объём выборки n и среднее квадратическое отклонение.
= 75,13; σ = 10; n = 100; γ = 0,95.

Решение

---

Задача 203tv

Найти доверительный интервал для оценки математического ожидания m нормального распределения с надёжностью 0,95, зная выборочную среднюю х, объём выборки n и среднее квадратическое отклонение.
= 75,14; σ = 9; n = 81; γ = 0,95.

Решение

---

Задача 893tv

Найти доверительный интервал для оценки математического ожидания m нормального распределения с надёжностью 0,95, зная выборочную среднюю х, объём выборки n и среднее квадратическое отклонение.
= 75,15; σ = 8; n = 64; γ = 0,95.

Решение

---

Задача 894tv

Найти доверительный интервал для оценки математического ожидания m нормального распределения с надёжностью 0,95, зная выборочную среднюю х, объём выборки n и среднее квадратическое отклонение.
= 75,16; σ = 7; n = 49; γ = 0,95.

Решение

---

Задача 895tv

Найти доверительный интервал для оценки математического ожидания m нормального распределения с надёжностью 0,95, зная выборочную среднюю х, объём выборки n и среднее квадратическое отклонение.
= 75,17; σ = 6; n = 36; γ = 0,95.

Решение

---

Задача 198tv

Найти доверительный интервал для оценки математического ожидания m нормального распределения с надёжностью 0,95, зная выборочную среднюю х, объём выборки n и среднее квадратическое отклонение.
= 75,09; σ = 14; n = 196; γ = 0,95.

Решение

---