| |||||||||||||||||||
| Специальный поиск | |||||||||||||||||||
|
|
|||||||||||||||||||
заряды поверхностными плотностями Задача 60178 С какой силой на единицу площади отталкиваются две одноименно заряженные бесконечные плоскости с одинаковой поверхностной плотностью заряда 41 нКл/кв.см. Задача 15123 Найти потенциал φ точки поля, находящейся на расстоянии r = 10 см от центра заряженного шара радиусом r = 1 см. Задачу решить, если: а) задана поверхностная плотность заряда на шаре σ = 0,1 мкКл/м2; б) задан потенциал шара φ0 = 300 В. Задача 15187 Шар, погруженный в керосин, имеет потенциал φ = 4,5 кВ и поверхностную плотность заряда σ = 11,3 мкКл/м2. Найти радиус R, заряд q, емкость С и энергию W шара. Задача 11755 Электрическое поле создано двумя бесконечными параллельными пластинами, несущими равномерно распределенный по площади заряд с поверхностными плотностями σ1 = 2 нКл/м2 и σ2 = –5 нКл/м2. Определить напряженность Е поля: 1) между пластинами; 2) вне пластин. Построить график изменения напряженности вдоль линии, перпендикулярной пластинам. Задача 26325 Непроводящий тонкий диск радиусом R = 10 см равномерно заряжен с одной стороны с поверхностной плотностью заряда σ = 15 нКл/см2. Диск вращается с угловой скоростью ω = 200 с–1. Найти магнитный момент системы. Задача 12079 Электрическое поле создано двумя бесконечными параллельными пластинами, несущими равномерно распределенные по площади заряды с поверхностными плотностями σ1 = 1 нКл/м2 и σ2 = –1 нКл/м2. Точка А находится между пластинами на расстоянии а = 1 мм от первой пластины. Определить: 1) величину и направление силы, действующей на заряд q = 0,1 нКл. помещенный в точку А; 2) разность потенциалов между точкой А и точкой B, лежащей на прямой, перпендикулярной к поверхностям пластин между ними на расстоянии d = 3 мм от точки А; 3) работу, совершаемую силами, перемещающими заряд q между указанными точками, и происходящее изменение его потенциальной энергии; 4) поток вектора напряженности через плоскость площадью S = 6 см2, расположенную в поле между пластинами под углом 30° к поверхностям пластин. Диэлектрическая проницаемость среды ε = 1. Задача 12682 Шар имеет потенциал φ = 4,5 кВ и поверхностную плотность заряда σ = 11,3 мкКл/м2. Найти радиус R, заряд q, емкость C и энергию W шара. Задача 13517 Разность потенциалов между длинными и тонкими коаксиальными цилиндрическими оболочками (R1 = 3 см и R2 = 10 см), заряженными равными разноименными зарядами, равна U = 450 В. Определить: а) заряд на единице длины оболочек; б) поверхностную плотность зарядов на каждой оболочке; в) напряженность вблизи поверхностей внутренней оболочки, на середине расстояния между оболочками и вблизи поверхностей внешней оболочки. Задача 14830 Сколько из приведенных выражений представляют энергию плоского заряженного конденсатора (в СИ)? Задача 15915 По поверхности сферического сегмента равномерно распределен электрический заряд с поверхностной плотностью σ = 60 нКл/м2. Определить в точке О, совпадающей с центром сферы напряженность Е электрического поля. Угол θ = π/4. Задача 16069 Пользуясь принципом суперпозиции электрических полей вычислить напряженность поля в точке, лежащей на перпендикуляре, восстановленном в центре заряженного диска, на расстоянии равном его радиусу. Поверхностная плотность заряда на диске 5 мКл/м2, радиус диска 0,05 м. Задача 20173 Две малые параллельные заряженные площадки S1 и S2 с одинаковой поверхностной плотностью зарядов σ ограничены одним телесным углом dΩ. Сравните напряженности E1 и E2 полей, создаваемых заряженными площадками S1 и S2 в вершине 0 телесного угла (r >> . Задача 20715 Два заряженных уединенных шара 1 и 2 соединены тонкой проволочкой, емкостью которой можно пренебречь. Отношение поверхностных плотностей заряда шаров σ1/σ2 = 0,5. Найдите отношение C1/C2 — емкостей шаров. Задача 21254 Предполагая в предыдущей задаче, что напряженность до заполнения парафином была E, найдите, каковы после заполнения значения электрической индукции и объемной плотности энергии в воздухе и парафине, а также какова поверхностная плотность заряда на парафине. Задача 22067 Шар, погруженный в масло (ε = 4), имеет потенциал φ = 4500 В и поверхностную плотность заряда σ = 10 мкКл/м2. Найти: 1) радиус R, 2) заряд θ, 3) емкость С, 4) энергию шара W. Задача 22833 Используя теорему Гаусса, найдите напряженность поля, создаваемого тонкостенным, бесконечно протяженным, металлическим цилиндром радиуса R = 5,0 см, как функцию расстояния r от оси цилиндра. Поверхностная плотность заряда цилиндра равна σ = 10 нКл/м2. Постройте график зависимости Е = f(r). Задача 22867 Поток электронов движется к заряженному шару радиусом 1 см в радиальном направлении. Какую линейную скорость должен иметь электрон на расстоянии 1 м от центра шара, чтобы достичь его поверхности, если поверхностная плотность заряда на шаре равна –10–10 Кл/м2? Определить ускорение электронов на расстоянии 0,5 м от центра шара. Задача 23864 Найти работу, которую необходимо совершить, чтобы перенести точечный заряд q = 42 нКл из точки, находящейся на расстоянии a = 1 м, в точку, находящуюся на расстоянии b = 1,5 см от поверхности сферы радиусом R = 2,3 см с поверхностной плотностью заряда σ = 4,3·10–11 Кл/м2. Задача 25206 Поверхностная плотность заряда σ бесконечно протяженной вертикальной плоскости равна 400 мкКл/м2. К плоскости на нити подвешен заряженный шарик массой m = 10 г. Определить заряд Q шарика, если нить образует с плоскостью угол φ = 30°. | |||||||||||||||||||
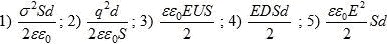
, где r — расстояние от площадки до вершины 0, S — величина площади площадки). 1) E1 = E2; 2) E1 < E2; 3) E1 > E2; 4) E1 >> E2.