| |||||||||||||||||||
| Специальный поиск | |||||||||||||||||||
|
|
|||||||||||||||||||
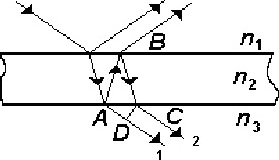
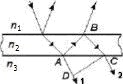
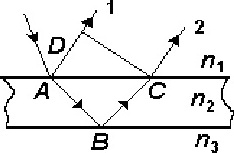
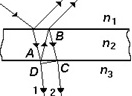
среде показателем преломления Задача 13946 Определите минимальную ускоряющую разность потенциалов Umin, которую должен пройти электрон, чтобы в среде с показателем преломления n = 1,5 возникло черенковское излучение. Задача 13945 Определите минимальную кинетическую энергию, которой должен обладать электрон, чтобы в среде с показателем преломления n = 1,5 возникло черенковское излучение. Ответ выразите в МэВ. Задача 13944 Определите минимальный импульс, которым должен обладать электрон, чтобы эффект Вавилова—Черенкова наблюдался в среде с показателем преломления n = 1,5. Задача 13942 Определите скорость электронов, при которой черенковское излучение происходит в среде с показателем преломления n = 1,54 под углом θ = 30° к направлению их движения. Скорость выразите в долях скорости света. Задача 14087 На тонкую плоскопараллельную пластинку падает световая волна. Волна 1, прошедшая через пластинку, и волна 2, отраженная от нижней и верхней поверхностей пластинки, интерферируют. Интерференция наблюдается в проходящем свете. Для показателей преломления сред выполняется соотношение n1= n3< n2. Задача 14240 Световой луч проходит путь L, причем часть пути r — в однородной среде с показателем преломления п = 1,33, другую часть пути r0 — в вакууме (n = 1). Оптическая длина пути луча наибольшая в случае, представленном под номером... . Задача 14267 На тонкую плоскопараллельную пластинку падает световая волна. Волна 1, прошедшая через пластинку, и волна 2, отраженная от нижней и верхней поверхностей пластинки, интерферируют. Интерференция наблюдается в проходящем свете. Для показателей преломления сред выполняется соотношение n1 = n3 < n2. Задача 14279 На плоскопараллельную пластику падает световая волна. Волна 1, прошедшая через пластинку, и волна 2, отраженная от нижней и верхней поверхностей пластики интерферируют. Интерференция наблюдается в проходящем свете. Для показателей преломления сред выполняется соотношение n1>n2>n3. Задача 14372 Световой луч проходит расстояние L: часть этого пути r0 — в вакууме (n = 1), другую часть пути r — в однородной среде с показателем преломления n = 1,5. В каком из приведенных ниже случаев оптическая длина пути наименьшая? Задача 16734 Расстояние от источника света до экрана равно L. Часть этого расстояния L1 = 2L/5 световой луч прошел в однородной среде с показателем преломления n, другую часть расстояния L2 = 3L/5 — в воздухе (nвоз0 = 1). Оптическая длина пути при этом оказалась равной l = 1,2L. Показатель преломления n среды равен... Задача 16735 Расстояние от источника света до экрана равно L. Часть этого пути L1 = 3L/5 световой луч прошел в однородной среде с показателем преломления n = 1,5, другую часть пути L2 = 2L/5 — в воздухе (nв = 1). Оптический путь l светового луча равен... Задача 16962 На плоскопараллельную пластинку падает световая волна. Волны 1 и 2, полученные в результате отражения от верхней и нижней поверхностей пластинки, интерферируют. Для показателей преломления сред выполняется соотношение n2 < n1, n2 < n3. Оптическая разность хода Δ21 волн 1 и 2 равна ... Задача 17148 Световой луч прошел расстояние L (геометрический путь), причем часть пути L1 = 2L/3 — в однородной среде с показателем преломления n, другую часть пути L2 = L/3 — в воздухе (nвозд = 1). Оптическая длина пути при этом оказалась равной l = 1,22L. Показатель преломления n среды равен... 1) 1,52 2) 1,45 3) 1,33 4) 1,22. Задача 19222 На тонкую плоскопараллельную пластинку падает световая волна. Волна (1), прошедшая через пластинку, и волна 2, отраженная от нижней и верхней поверхностей пластинки, интерферируют. Интерференция наблюдается в проходящем свете. Для показателей преломления сред выполняется соотношение n1<n2<n3. Оптическая разность хода Δ21 волн 1 и 2 равна... Задача 19230 Оптическая разность хода двух волн, прошедших одинаковое расстояние L, если одна распространялась в вакууме, а другая — в среде с показателем преломления n, равна ... Задача 19233 Световой луч проходит расстояние r в однородной среде с показателем преломления n = 1,5 и расстояние r0 в вакууме (n = 1). В каком из указанных ниже случае оптическая длина пути луча больше? Задача 19697 Световой луч проходит расстояние r в однородной среде с показателем преломления n = 1,5 и расстояние r0 в вакууме (n = 1). В каком из указанных ниже случаев оптическая длина пути луча меньше? Задача 19709 Световой луч проходит путь L, причем часть пути r — в однородной среде с показателем преломления n = 1,5, другую часть пути r0 — в вакууме (n = 1). Оптическая длина пути луча наименьшая в случае, представленном под номером ... Задача 19710 Световой луч прошел расстояние L (геометрический путь): часть этого расстояния L1 = L/2 в однородной среде с показателем преломления n, другую часть L2 = L/2 — в воздухе (nвозд = 1). Оптический путь луча оказался равным l = 1,25L. Показатель преломления n среды равен ... | |||||||||||||||||||
