| |||||||||||||
| Специальный поиск | |||||||||||||
|
|
|||||||||||||
постоянное тангенциальное ускорение Задача 13089 Материальная точка массой m = 20 г движется по окружности радиусом R = 10 см с постоянным тангенциальным ускорением. К концу пятого оборота после начала движения кинетическая энергия материальной точки оказалась равной 6,3 мДж. Определить тангенциальное ускорение. Задача 15996 За промежуток времени τ = 10,0 с точка прошла половину окружности радиуса R = 160 см. Вычислить за это время: а) среднюю скорость (v); б) модуль среднего вектора скорости |< Задача 40503 За промежуток времени τ = 10,0 с частица прошла половину окружности радиусом R = 160 см с постоянным тангенциальным ускорением. Вычислить за это время а) средний модуль скорости |< Задача 40804 Материальная точка начинает двигаться без начальной скорости по окружности радиусом R = 20 см с постоянным тангенциальным ускорением aτ = 5 см/с2. Через какое число оборотов после начала движения нормальное ускорение точки станет равным тангенциальному? Задача 11007 Точка движется по кривой с постоянным тангенциальным ускорением аτ = 0,5 м/с2. Определить полное ускорение а точки на участке кривой с радиусом кривизны R = 3 м, если точка движется на этом участке со скоростью v = 2 м/с. Задача 26047 Первоначально покоившееся тело прошло за время t = 10 с полторы окружности радиуса R = 5 м с постоянным тангенциальным ускорением. Вычислить соответствующие этому промежутку времени значения: а) среднего модуля скорости <v>, б) модуля средней скорости |<v>|, в) модуля среднего ускорения |<a>|. Задача 13305 Материальная точка начинает двигаться по окружности радиусом r = 12,5 см с постоянным тангенциальным ускорением аτ = 0,5 см/с2. Определите: 1) момент времени, при котором вектор ускорения а образует с вектором скорости v угол α = 45°; 2) путь, пройденный за это время движущейся точкой. Задача 20205 Материальная точка начинает двигаться по часовой стрелке по окружности радиусом R = 10 см с постоянным тангенциальным ускорением аτ = 0,4 см/с2. Через промежуток времени t вектор полного ускорения а образует с вектором мгновенной скорости v угол β = 60°. Определить t. Задача 20206 Материальная точка начинает двигаться по часовой стрелке по окружности радиусом R = 20 см с постоянным тангенциальным ускорением аτ. Через промежуток времени t = 5,0 с вектор полного ускорения а образует с вектором мгновенной скорости v = 0,02 м/с угол β. Определить a. Задача 20207 Материальная точка начинает двигаться по часовой стрелке по окружности радиусом R = 30 см с постоянным тангенциальным ускорением аτ = 0,5 см/с2. Через промежуток времени t вектор полного ускорения а образует с вектором мгновенной скорости v угол β = 45°. Определить v. Задача 20208 Материальная точка начинает двигаться по часовой стрелке по окружности радиусом R с постоянным тангенциальным ускорением аτ. Через промежуток времени t = 6,5 с вектор полного ускорения а = 0,8 см/с2 образует с вектором мгновенной скорости v = 0,03 м/с угол β. Определить β. Задача 20209 Материальная точка начинает двигаться по часовой стрелке по окружности радиусом R = 50 см с постоянным тангенциальным ускорением аτ = 0,5 см/с2. Через промежуток времени t вектор полного ускорения а = 0,9 см/с2 образует с вектором мгновенной скорости v угол β. Определить v. Задача 25662 Материальная точка начинает движение по окружности радиусом R = 23,7 см с постоянным тангенциальным ускорением aτ = 5,32 см/с2. Спустя какое время нормальное ускорение будет в 5,00 раз больше тангенциального? | |||||||||||||
 >|; в) модуль среднего вектора полного ускорения |<
>|; в) модуль среднего вектора полного ускорения |< >|, если точка двигалась с постоянным тангенциальным ускорением.
>|, если точка двигалась с постоянным тангенциальным ускорением.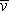 >|; б) модуль среднего вектора полного ускорения |<
>|; б) модуль среднего вектора полного ускорения |< >|.
>|.